Quantum Control Theory

Applications in quantum information science require precise control of the dynamics of complex quantum systems. This control is typically achieved through shaped electromagnetic fields, as depicted in the Figure. Quantum control theory offers an excellent framework for meeting this challenge. Our research is centered around the mathematical description of quantum control and the design of effective strategies for achieving a desired control task in a noise robust and optimal fashion. Research efforts include studying what we can do with the system at hand given a set of controls [1,2], characterizing the time and energy scales needed to carry out a desired control task [3,4], determining what we can learn about the system from output signals [5,6], and designing control algorithms that find effective control solutions [7,8]. Target applications include improving the implementation of quantum gates and high-fidelity state preparation for quantum information tasks.
[1] C. Arenz, G. Gualdi and D. Burgarth, New J. Phys. 16, 065023 (2014), arXiv:1312.0160.
[2] C. Arenz, D. Burgarth, P. Facchi, V. Giovannetti, H. Nakazato, S. Pascazio and K. Yuasa, Phys. Rev. A 93, 062308 (2016), arXiv:1601.01212
[3] C. Arenz, D. Burgarth, B. Russell and H. Rabitz, New J. Phys. 19, 103015 (2017), arXiv:1704.06289
[4] C. Arenz and H. Rabitz, Phys. Rev. Lett. 120, 220503 (2018), arXiv:1710.02579
[5] P. Yang, M. Yu, R. Betzholz, C. Arenz, and J. Cai, Phys. Rev. Lett. 124, 010405 (2020), arXiv:1909.09980
[6] C. Arenz and H. Rabitz, Phys. Rev. A 102, 042207 (2020), arXiv:2004.02729
[7] Q.-M. Chen, X. Yang, C. Arenz, R. Wu, X. Peng, I. Pelczer, and H. Rabitz, Phys. Rev. A 101, 032313 (2020), arXiv:1812.05042
[8] X. Yang, C. Arenz, I. Pelczer, Q.-M. Chen, R. Wu, X. Peng, and H. Rabitz, Phys. Rev. A 102, 062602 (2020), arXiv:2008.03874
Quantum algorithms for near term quantum computers
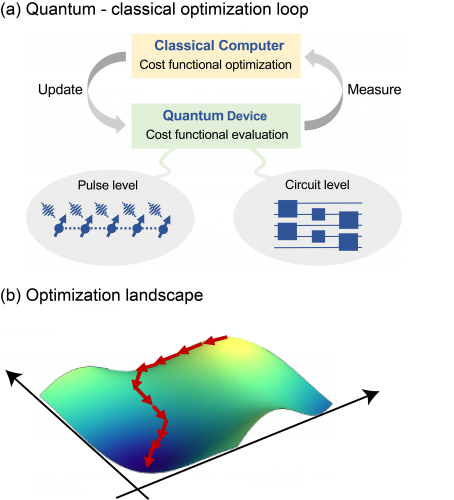
Quantum algorithms that run on current quantum devices typically use quantum and classical computing resources in parallel, as depicted in Figure (a). Within this setting, the quantum device can be treated as a complex controlled dynamical system whose control inputs correspond to shaped electromagnetic pulses, while the output is the solution to a high value problem [1]. Taking this dynamical systems perspective allows for improving quantum device performance by working at the pulse level at which detrimental dynamical processes can be mitigated. Rather than abstracting away from the physics and operating at the circuit level, by working at the pulse level of quantum devices, our research aims to design strategies that mitigate decoherence, that increase robustness to noise, and that allow for scaling up the system while maintaining coherence. Meanwhile, we use tools from classical non-convex optimization to design quantum algorithms with enhanced convergence properties and noise robustness. Here, the interplay between the underlying optimization landscape structure (Figure (b)), the problem instance at hand, and the quantum algorithm ansatz used to solve the problem under consideration, all play an essential role [2,3].
[1] A. Magann, C. Arenz, M. Grace, T.-S. Ho, R. Kosut, J. McClean, H. Rabitz, and M. Sarovar, PRX Quantum 2, 010101 (2021), arXiv:2009.06702
[2] J. Lee, A. Magann, H. Rabitz, and C. Arenz,
Progress toward favorable landscapes in quantum combinatorial optimization
Phys. Rev. A 104, 032401 (2021), arXiv: 2105.01114
[3] R. Kosut, C. Arenz, and H. Rabitz, J. Phys. A: Math. Theor. 52 165305 (2019), arXiv:1810.04362
Driven many-body systems
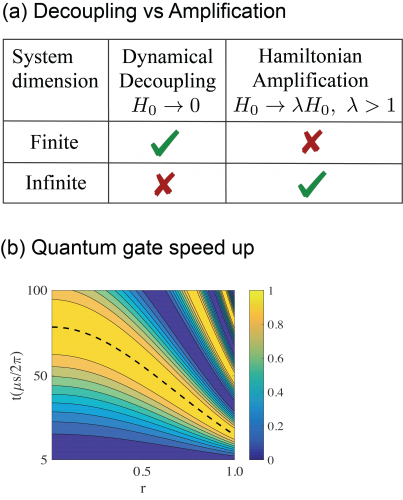
The dynamics of quantum systems with many constituents can exhibit rich and sometimes surprising behavior. From dynamical phase transitions and localization to decoherence in quantum systems that interact with a large environment, these effects have in common that they typically appear in systems with many degrees of freedom. At the heart of this research thrust lies the question of how to control or engineer these effects through external classical drives. A prominent example is dynamical decoupling that allows for suppressing interactions through periodic drives of high frequency [1-3], thereby effectively engineering the Hamiltonian of a complex system. Based on parametric periodic drives, we recently developed a protocol that achieves the opposite, i.e., it enhances desired interactions so that the system dynamics is sped up, which we dubbed “Hamiltonian Amplification’’[4], as depicted in Figure (a). Current research efforts are centered around investigating how both schemes can be combined to suppress unwanted interactions while desired interactions are enhanced, e.g., to speed up the implementation of quantum gates (Figure (b)). We further investigate whether these protocols can be used to engineer and explore many-body effects. Moreover, we are also utilizing random drives to analyze how quantum information propagates through multi qubit networks [5].
[1] C. Arenz, R. Hillier and D. Burgarth, J. Phys. A: Math. Theor. 50, 135303 (2016), arXiv:1605.05908
[2] C. Arenz, D. Burgarth, P. Facchi and R. Hillier, J. Math. Phys. 59, 032203 (2018), arXiv:1704.06143
[3] C. Arenz, R. Hillier, M. Fraas and D. Burgarth, Phys. Rev. A 92, 022102 (2015), arXiv:1405.7644
[5] C. Arenz, D. I. Bondar, D. Burgarth, C. Cormick and H. Rabitz, Quantum 4, 271 (2020), arXiv:1806.00444
[6] P. Yang, M. Yu, R. Betzholz, C. Arenz, and J. Cai, Phys. Rev. Lett. 124, 010405 (2020), arXiv:1909.09980

